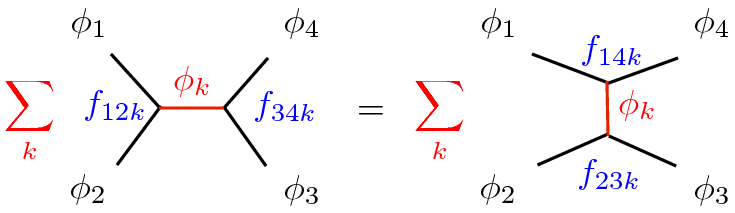1. What is the space of CFTs?
The long distance dynamics of a quantum field theory is captured by conformal field theory. One of the great insights of the 20th century is that the space of CFTs is highly constrained: wildly different microscopic systems can be described by the same CFT at long distances. This is the phenomenon of critical universality. We can then hope to achieve a naively absurd dream: solve the long-distance dynamics of any QFT. All we must do is classify and solve CFTs. Then, given a specific physical system, we simply ask which member of the classification it corresponds to. This strategy, articulated by Ferrara, Gatto, Grillo, and Polyakov in the 1970's, is the conformal bootstrap. The logic is so robust that it applies in virtually all areas of theoretical physics. Problems in particle physics, condensed matter physics, statistical physics, and quantum gravity can all be solved by a classification of CFTs.
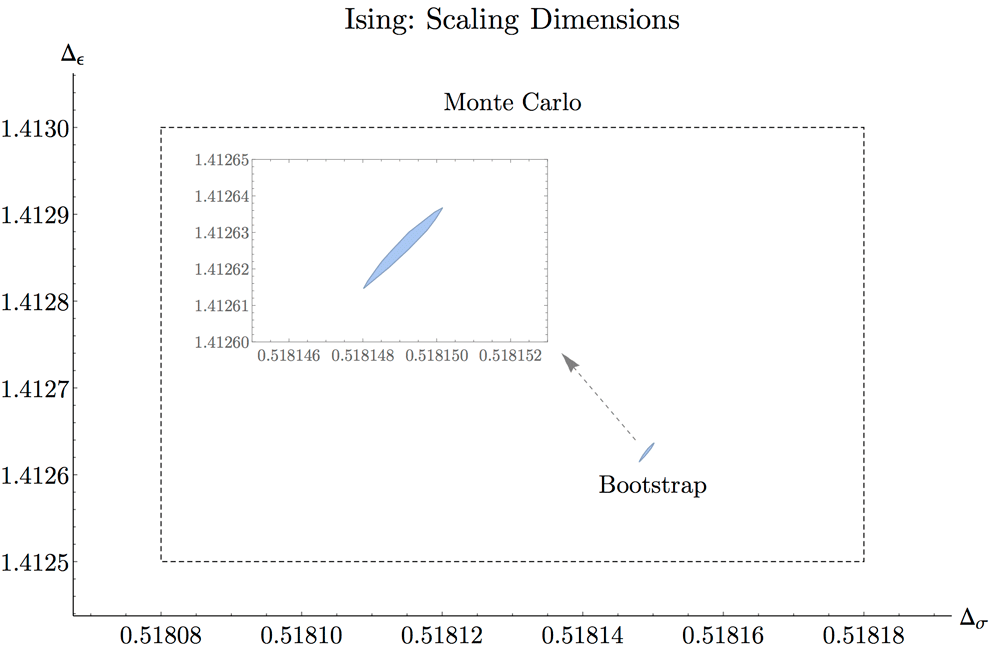
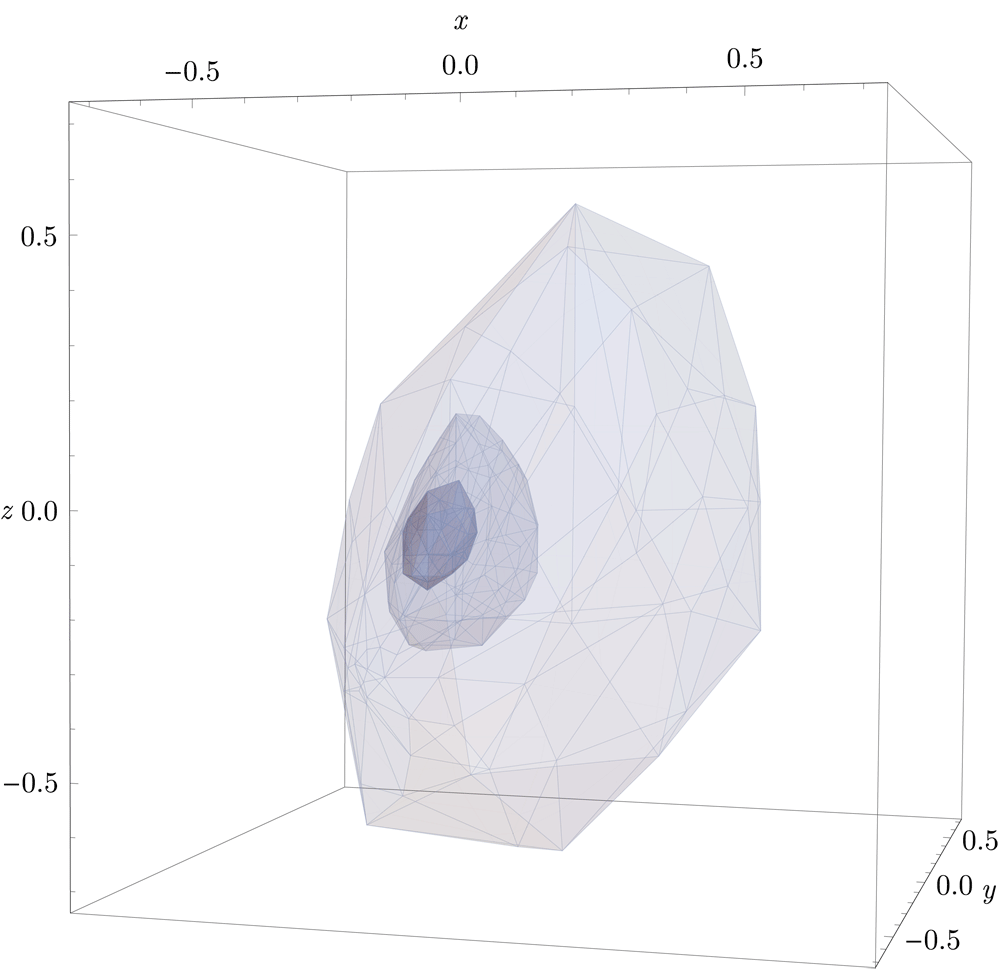
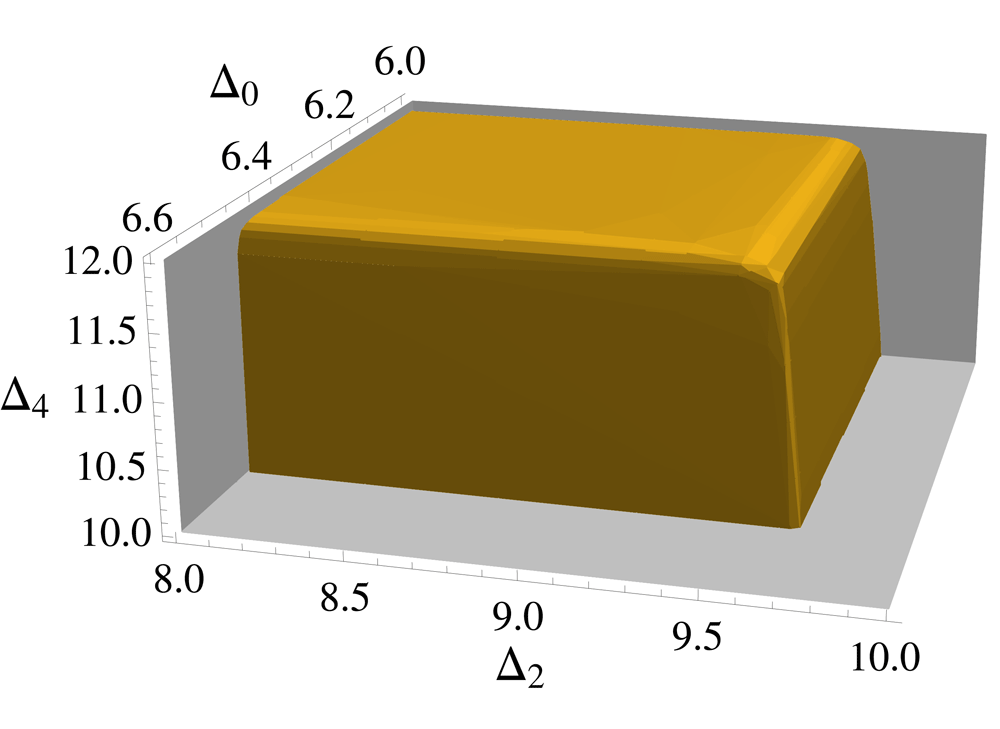
While a partial classification of 2d CFTs was achieved in the 1980's and 1990's, only now do we have the tools to attempt a similar classification in higher dimensions. Natural organizing principles for our classification are symmetries and the number of relevant operators. Using numerical bootstrap techniques, we can now take a symmetry group and set of relevant operators and produce precise information about observables of CFTs with those properties. A major goal of our collaboration is to obtain the full catalog of CFTs with a small number of relevant operators in various dimensions. This catalog would have profound implications for condensed matter and statistical physics. We have dubbed this enterprise the CFT genome project. We have already succeeded in mapping out simple cases, like 3d CFTs with Z2 symmetry and two relevant operators - leading to the most precise determination to date of the 3d Ising critical exponents - and we are beginning to understand the space of theories with O(N) symmetry. Major targets for the CFT genome project are the solution of 3d QED and the determination of the conformal window of 4d QCD.
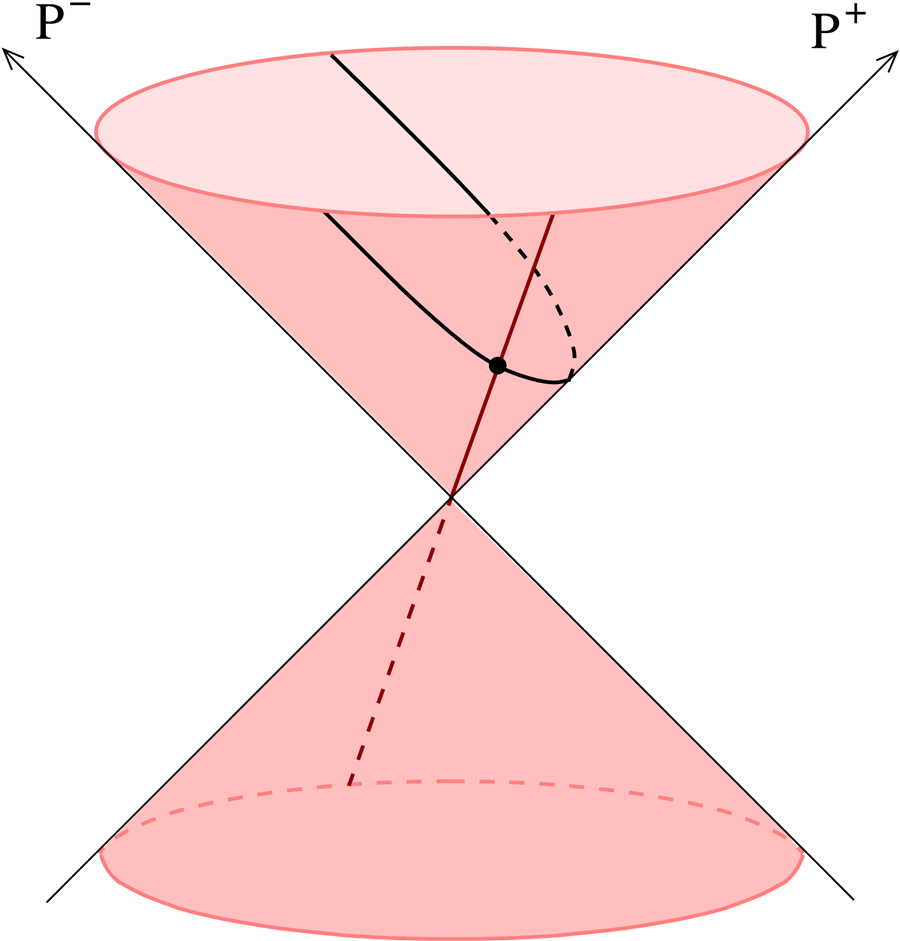
2. What is the space of QFTs?
A general QFT can be viewed abstractly as an RG flow, specified by the initial point (the UV CFT) and a starting direction (the relevant perturbing operators). The problem is then to determine the long-distance theory. Is it gapless or gapped? What are the masses of the particles? What is their scattering S-matrix? Since most interesting flows are nonperturbative, there are few cases where these questions can be answered analytically. In general, as in QCD, one has to rely on costly numerical Monte-Carlo simulations on the lattice, and even then many of the most interesting questions are unanswerable.
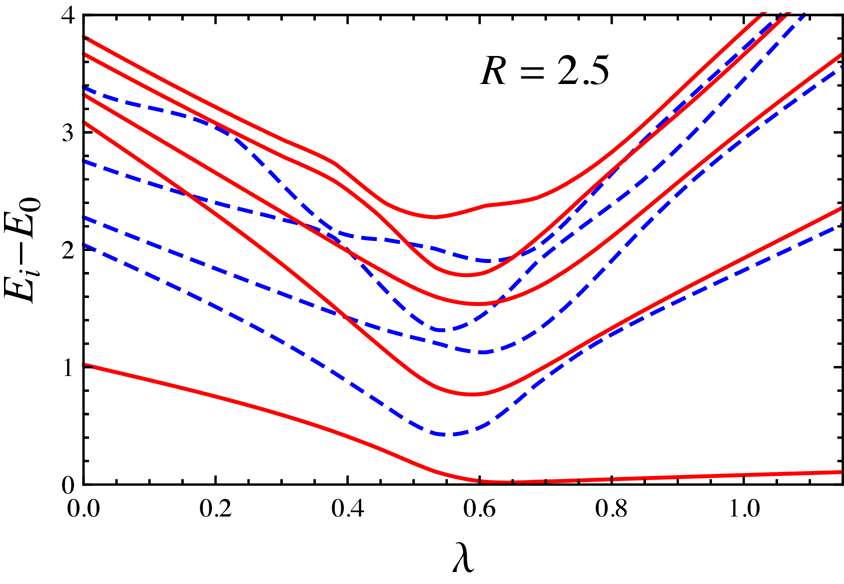
Moreover, we would like to study flows which start at a CFT defined, in the spirit of the conformal bootstrap, just in terms of abstract data about operator dimensions and OPE coefficients, instead of a Lagrangian. This can be achieved by Hamiltonian truncation techniques, which generalize the well-known Rayleigh-Ritz method from Quantum Mechanis to QFT. One idea is the truncated conformal space approach (TCSA), proposed by Yurov and Zamolodchikov back in 1989 for perturbations of (1+1)d CFTs, and recently extended to d>2. Another promising truncation arises when QFT is quantized on the light-cone, which offers advantages of eliminating vacuum divergences and allowing calculations directly in the infinite volume limit. By developing these ideas further we hope to approach our long-term dream: mapping out not only the CFTs, signposts in the space of quantum field theories, but also the roads - RG flows - connecting these signposts.
An alternative to the above is to solve the long-distance theory by writing down the consistency conditions satisfied by the S-matrix of its particles. This S-matrix bootstrap program historically predates the conformal bootstrap, but it was largely abandoned in the 70s (although it gave birth to string theory and is behind the modern theory of perturbative scattering amplitudes). However, very recent work by members of our collaboration has revived the non-perturbative S-matrix bootstrap, as well as provided an intriguing connection with the conformal bootstrap. We expect rapid progress in this direction.
3. Can we classify and solve supersymmetric field theories?
Supersymmetric quantum field theories provide an ideal theoretical laboratory for the study of QFT and have deep connections with string theory and contemporary mathematical physics. A complete classification of superconformal field theories (SCFTs) appears much more attainable than for non-susy CFTs. Spaces of SCFTs are equipped with geometrical structure, and in some cases their classification is closely tied to that of natural mathematical objects such as algebraic curves or vertex algebras. In the SCFT landscape there exist many isolated models with no conventional Lagrangian description. The paradigmatic examples are the (2,0) supersymmetric theories in six spacetime dimensions, which are central to many recent developments in formal quantum field theory. Yet their non-Lagrangian nature makes it very difficult to compute even the most basic observables. Our collaboration promotes an operator-algebraic viewpoint: theories are defined by their abstract algebras of (local or non-local) operators. This viewpoint applies to Lagrangian or non-Lagrangian theories alike, and it is the only way to carry out a comprehensive classification program.
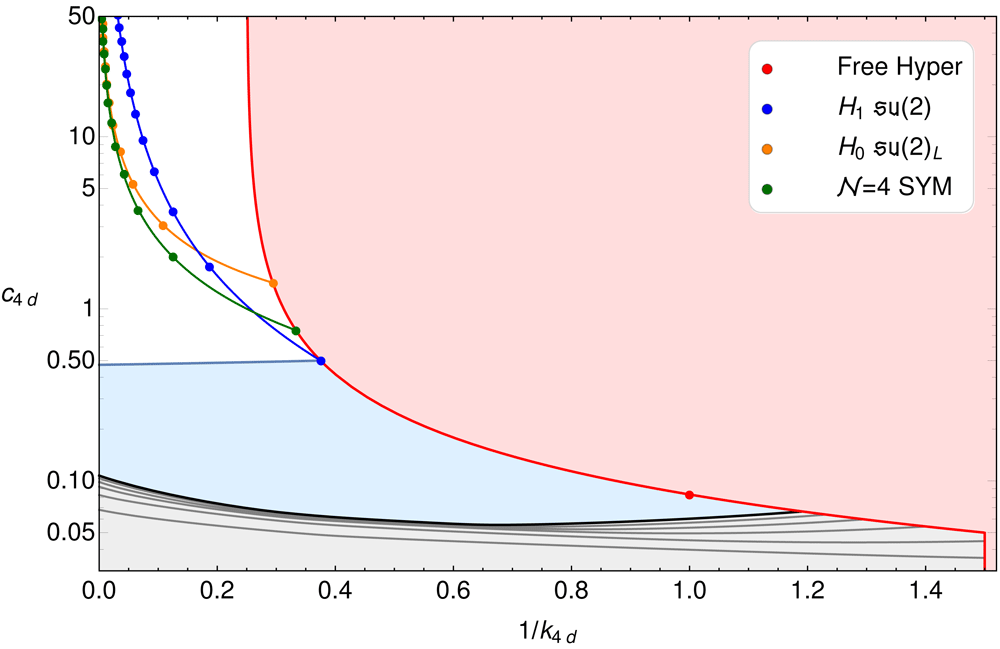
We have already obtained clear proofs of concept that numerical bootstrap techniques are very effective for SCFTs. Highlights include the first truly non-perturbative results for maximally supersymmetric theories in three, four and six dimensions. We plan to develop the analytic and computational tools for a systematic exploration of the landscape of SCFTs and for the precise numerical solution of concrete models of particular importance, such as the N=4 super Yang-Mills (SYM) theories and the (2,0) theories. What’s more, supersymmetry facilitates the derivation of exact results. This leads to a complementary research direction, where analytic rather than numerical approaches take center stage. For example, it is often possible to exactly solve entire subsectors of the operator algebra. These subsectors take the shape of a chiral or topological algebra, and their classification will provide a springboard for the full-fledged classification of SCFTs. In another development, it has been shown recently that correlation functions of chiral operators in two and four dimensions are subject to integrable equations, even though the theory itself is not integrable. In planar N=4 SYM theory the underlying integrability makes even a complete analytic solution of the theory a realistic goal.
4. How does quantum gravity emerge from the bootstrap?
Gravity was the first force to be described quantitatively, but despite a century of effort, fundamental problems plague the quantum theory. Of the myriad issues involved, none is more emblematic than the black hole information paradox: in Einstein's theory of general relativity, black holes destroy information, contradicting the basic tenets of quantum mechanics. At present we know of only one complete definition of quantum gravity that fully reconciles these issues: the profound holographic equivalence between CFT and gravity in a higher-dimensional Anti-de Sitter (AdS) space. Thus it appears that the key to quantum gravity is buried in the landscape of non-gravitational CFTs.
Nevertheless, while the broad outlines of how CFTs successfully merge general relativity and quantum mechanics are clear, many essential details remain obscure. Only recently have we begun to understand how and when CFTs effectively "grow" an extra dimension governed by local physics and Einstein's equations. Conformal bootstrap techniques can be used to constrain and probe the dynamics of the higher-dimensional gravity theory, indicating when a local spacetime - no longer a fundamental quantity - emerges as an approximation. Combined with additional techniques available in 2d CFTs, conformal bootstrap methods have elucidated the microscopic origin of black hole temperature and entropy in 3d gravity, have led to a sharp new formulation of black hole information loss, and suggested steps towards its resolution. Ultimately, our collaboration aims to use these 2d CFT results as a foundation to generalize to higher dimensions by combining them with recent progress on strongly-coupled CFTs using supersymmetry and integrability.
5. The unreasonable effectiveness of the bootstrap
The success of modern bootstrap techniques has surpassed all expectations. Numerical bootstrap methods were originally intended to place simple one-sided bounds on CFT data. However, we now understand that these bounds are sometimes powerful enough to completely isolate specific theories (like the 3d Ising model), and determine their observables to high precision. It is poorly understand when and why this happens.
Clarifying and extending the mechanisms behind numerical bootstrap bounds will be a crucial step in achieving our goal of mapping out the space of CFTs. Given a specific theory, we would like to know: What information about that theory must be incorporated into the bootstrap to completely isolate it? For which theories can we compute high-precision bounds similar to those achieved in the 3d Ising model? Answering these questions will require both numerical exploration and analytical work. Unlike lattice Monte Carlo, the numerical bootstrap is also an analytical technique — numerics are necessary only to improve the precision, by combining multiple analytical constraints, it may eventually be possible to eliminate the reliance on numerics altogether.
From a more mathematical perspective, we would like to know if an operator-algebraic approach can provide a mathematically rigorous definition of CFT, or even of QFT more generally. This is already the case for 2d rational CFTs and 3d topological QFTs, where the operator algebra is finite-dimensional, but it seems likely that new rigorous theorems could be proven outside of this limited situation. We have already made progress by proving rigorous bounds on OPE convergence, mapping sectors of SCFTs to solvable chiral algebras, and developing the idea of effective CFTs, where a finite-dimensional truncation can be used to compute observables for low-lying CFT states. By making the concept of an effective CFT mathematically precise, we believe it should be possible to turn questions about how much error is induced by the truncation into well-defined questions in real analysis.